基本情報技術者試験の最大の難関はアルゴリズム問題です。
アルゴリズムの解説や勉強法、コツを検索すると「トレースしましょう」と言われます。
たしかに、問題文の意味を理解し、プログラムの動き通りに考え、丁寧にトレースすれば全問正解も容易でしょう。
しかし、問題文の解釈が難しい!プログラムの動きが分からない!穴埋めが分からない!丁寧にトレースする時間がない!と多くの人がなるはずです。
私もそうでした。解説を読めば何となく分かるけど解き方が分からない!という状態で、どうやって読めば本番で合格できるのだろう..と悩んでいました。
そこで、基本情報技術者試験の一合格者として、実際に解く際に「どこに着目して、どういうメモを取って、どういう風にトレースしているのか」を解説してみようと思いました。
本記事では平成31元年春期の過去問を使います。
参考書や各種サイトの丁寧で完璧な解説ではなく、合格者のノートや手元を覗き見る気持ちで読んでください。
導入部分を読む
はじめに「どんなことをするプログラムなのかな?」を確認してみましょう。

「ハフマン符号化」という方法による文字列圧縮に関する問題のようです。
この時点で「ハフマン符号化」を知らなくても、文中の説明を読んで理解できればOKです。
具体例が出てくるのでこのまま読み進めます。

(1)~(4)で具体的な文字列を使って「ハフマン符号化」の手順について解説してくれるようです。
この時点ではプログラムは無関係なのと、設問1では下記の通り別の文字列を使っているので「日本語ベースで流れを理解する」ことを意識しましょう。
設問で別の文字列を使うなら..と飛ばしたくなるかもしれませんが、出題者が我々受験生のために「わざわざ準備してくれている」ということなので、これに従って理解するのが吉です。

試験の勉強を進めている方は「枝」「節」「根」「葉」は既知の単語だと思いますが、まだ始めたばかりで初見の方はせっかくの機会なので覚えてしまいましょう!
文章だけだとわかりにくいですが、問題の中に図も用意してくれています。
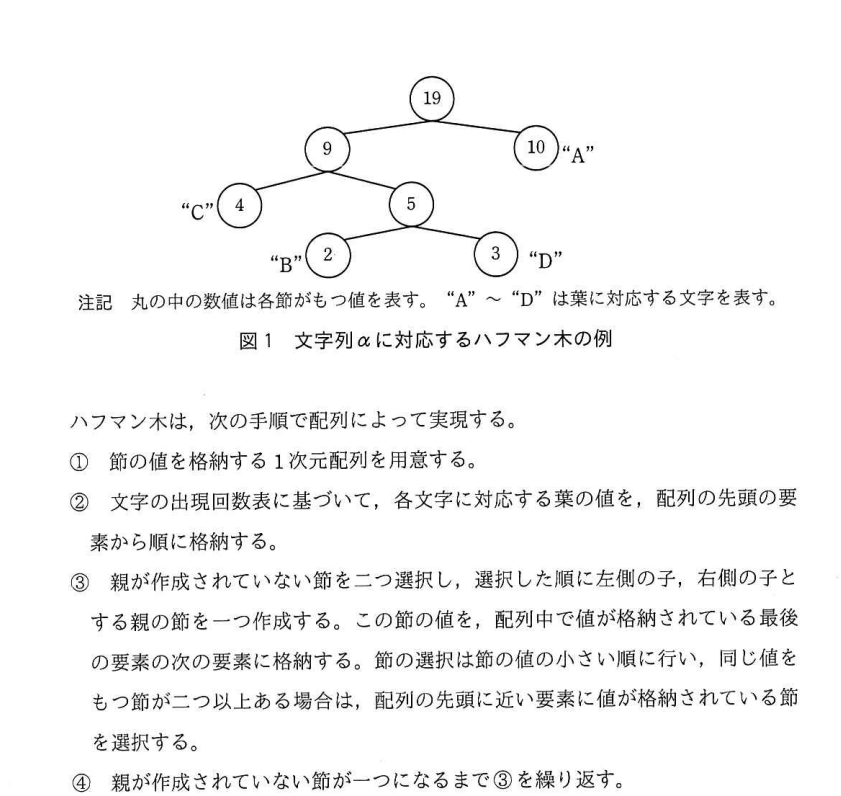
既に図はありますが、①~④の手順に従って自分のメモに書いてみると理解が深まるのでおすすめです。
手順に沿ってハフマン木の生成方法を確認する
一緒に書いていきましょう。まずは①と②です。
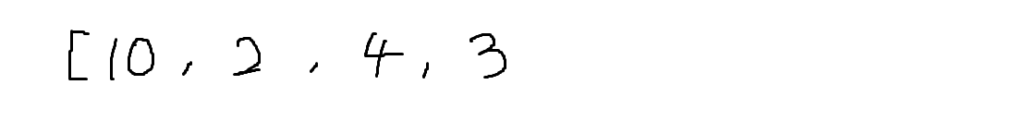
これは表1を配列にしただけですね。続けて③を見ていきます。
現時点では親はどれも生成されていないので、値の小さい2番目と4番目を選び新しい節を作ります。
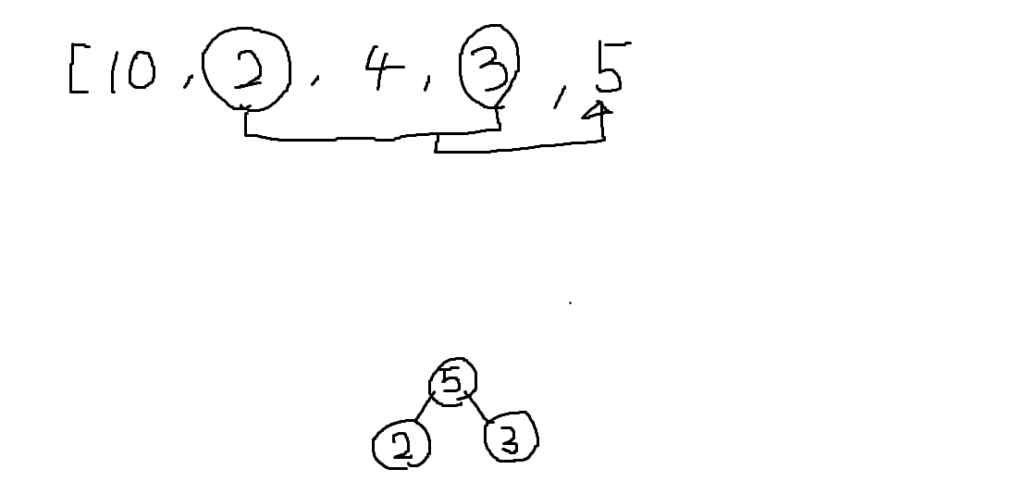
1番、3番、5番がまだ親がいないので、もう一度③を繰り返します。
今回は3番と5番が小さい値なので、これらから新しい節を作ります。
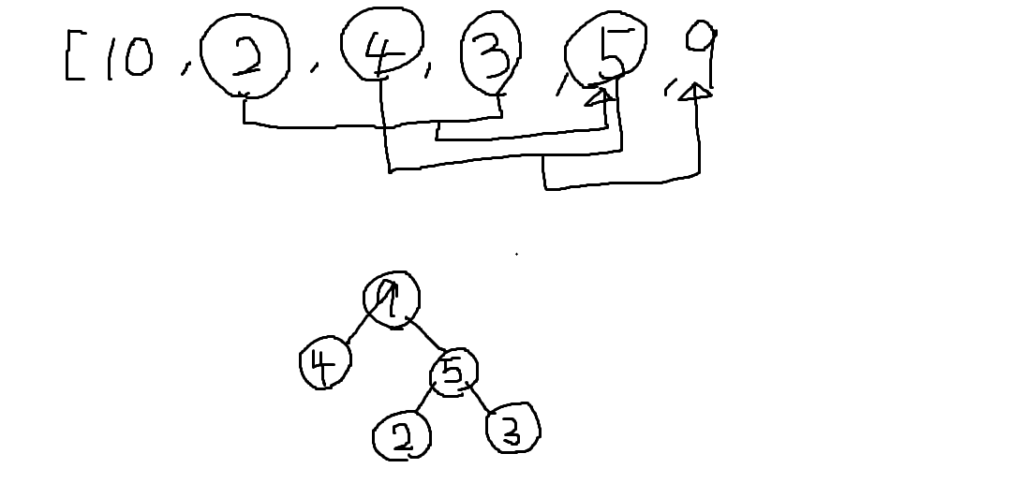
同様に1番と6番で新しい節を作ると「親がいない節が一つ」になるので終了です。
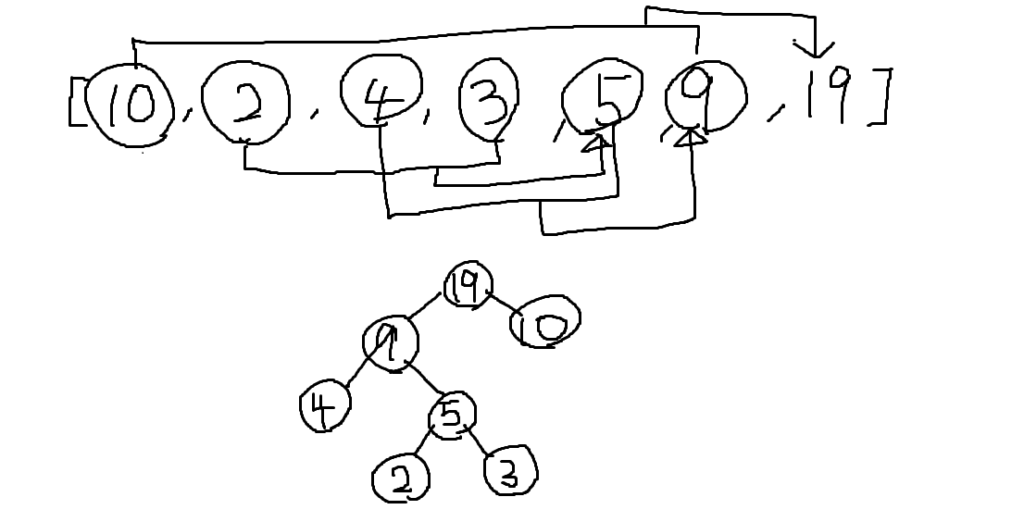
これでハフマン木は完成です。。
手順が理解できれば文字列が変わっても対応できますし、プログラムに落とし込んだ際もソースコードと日本語の対応付けが容易にできます。
続いて手順を参考にビット列を作成してみましょう。
手順に沿ってビット列の生成方法を確認する
作成したハフマン木を使って以降の手順を確認していきます。

「枝」は節と節をつなぐ線です。この上に0または1を書くと、図2と同じものが完成します。(メモは割愛しますね。)
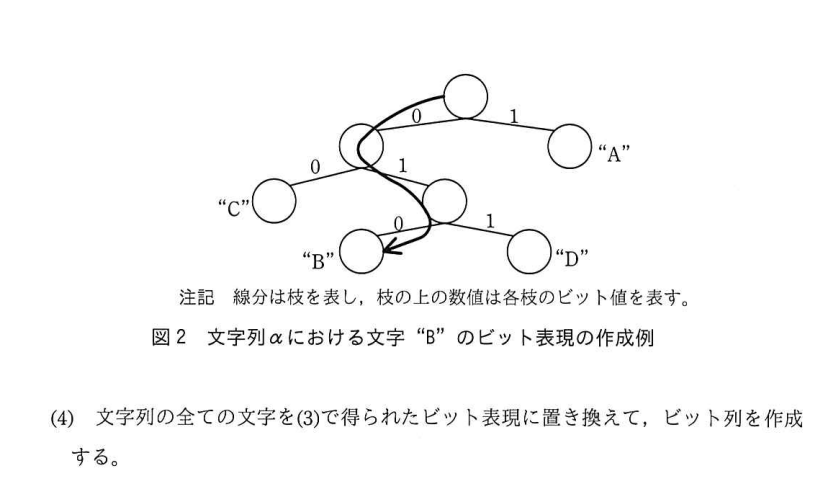
Aなら「1」、Bなら「010」、Cなら「00」、Dなら「011」となります。
出現回数の多いAは1ビットで表現できることになります。
設問1を解く
ハフマン木の作成手順、ビット列の作成手順の確認ができたので早速問題に取り掛かりましょう。
導入部分は日本語だけなのでここまで5分程度で来れていると順調な滑り出しといえます。
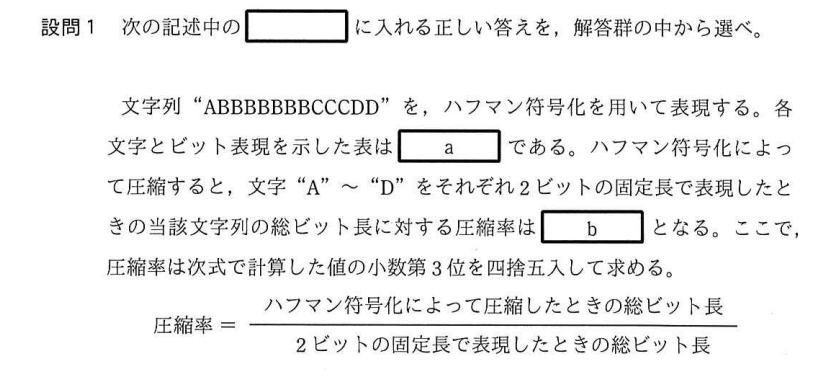
文字列が導入部分と異なってるので新しくハフマン木を作成してみましょう。
ハフマン木生成の①、②を設問の文字列で実施するとこのようなメモが完成します。

ここから値の小さい(出現回数の少ない)2つを選び新しい節を作ります。
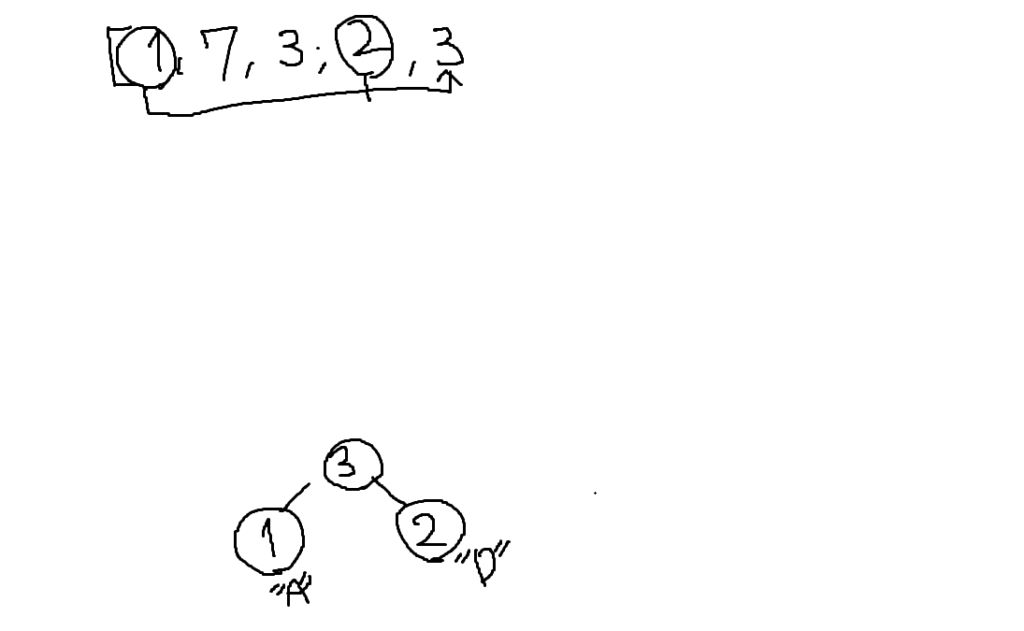
ハフマン木を上方向に書くのでスペースを空けています。
まだ親がいない節が2つ以上あるので、もう一度値の小さい節から新しい節を作ります。
今回は「3」という同じ値がありますが、先頭に近い方から選択していきます。
よって今回は文字Cの出現回数である「3」が左側の子としてハフマン木を作成します。
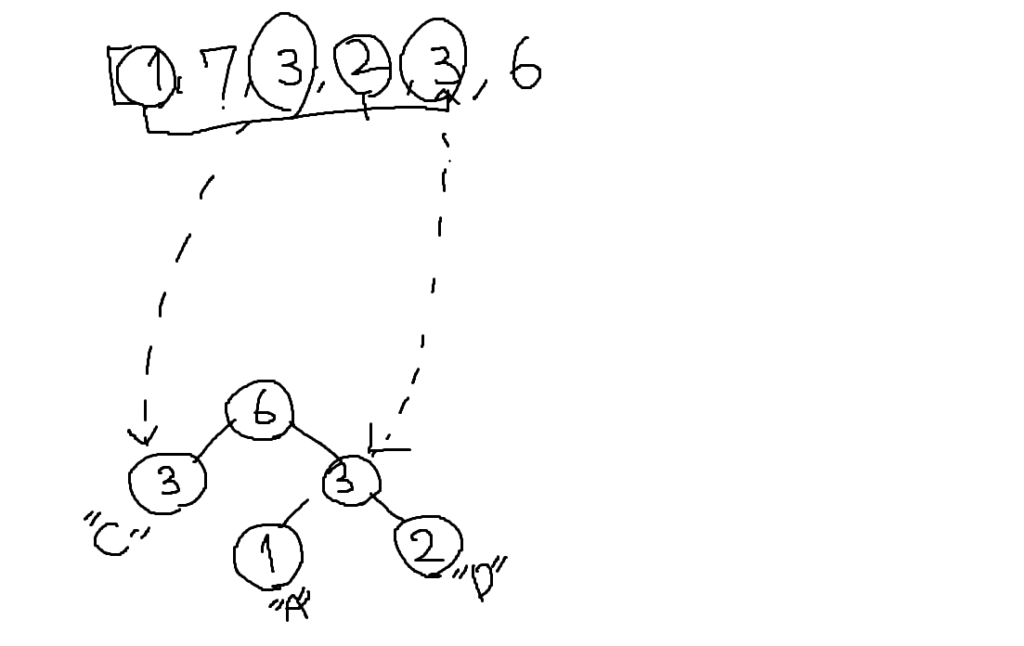
もう一度親の節を作るとハフマン木は完成です。
同時に左の枝に0、右の枝に1を入れたメモが以下になります。
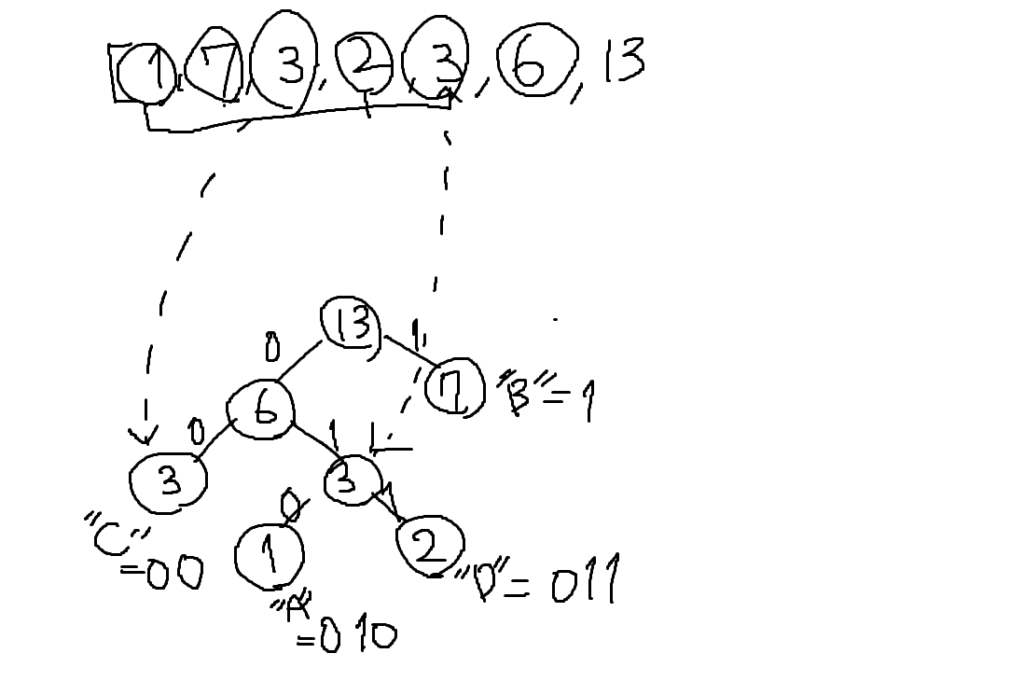
選択肢と見比べると「ア」が正解になることが分かります。
次に圧縮率を計算します。
総ビット長は「文字数」×「その文字のビット長」で求められます。
まず2ビット固定の場合は「総文字数(13)×ビット長(2)」のため26になります。
圧縮後はAとDなら3ビット、Cなら2ビット、Bなら1ビットというように文字ごとにビット長を求め、その総和が総ビット長になります。
式は、A文字数(1)×Aビット長(3) + B文字数(7)×Bビット長(1) + C文字数(3)×Cビット長(2) + D文字数(2)×Dビット長(3)となるので、総ビット長は22ビットになります。
これらを圧縮率の式に当てはめ、22÷26=0.846….なので答えは「イ」です。
設問2を解く
次の問題に進みます。

ハフマン木の生成をプログラムでやりましょう!という内容で、設問的にはプログラムの穴埋めだけのようです。
先に選択肢とプログラムの空欄箇所を見てみると、どちらも「条件」を選ぶようです。

選択肢から「nsize」、「size」という変数と「parent[i]」という配列の値がキーとなることが読み取れます。
プログラムの説明およびプログラムを読む際は上記の変数・配列と処理条件を意識して読むと良いです。
複雑そうなプログラムや変数がたくさんある場合は先に選択肢を確認して、「内容がある程度わかれば流し読みしてもOKな部分」と「解答に直結する丁寧に理解・トレースする部分」をしっかり区別することが短時間でアルゴリズム問題を攻略するコツです!
これらを念頭にまずはプログラムの説明から読んでいきます。
プログラムの説明を読む

なんと配列が4つも出てきてしまいました。
この後に図表が出てくるので、この時点でのメモは不要です。
が、「-1」で初期化は覚えておくかメモしておく価値はあります。
理由はこの後プログラムを読んだ際、プログラムの最初の方で「-1」があればそのブロックは初期化処理だなとすぐに判断できるからです。
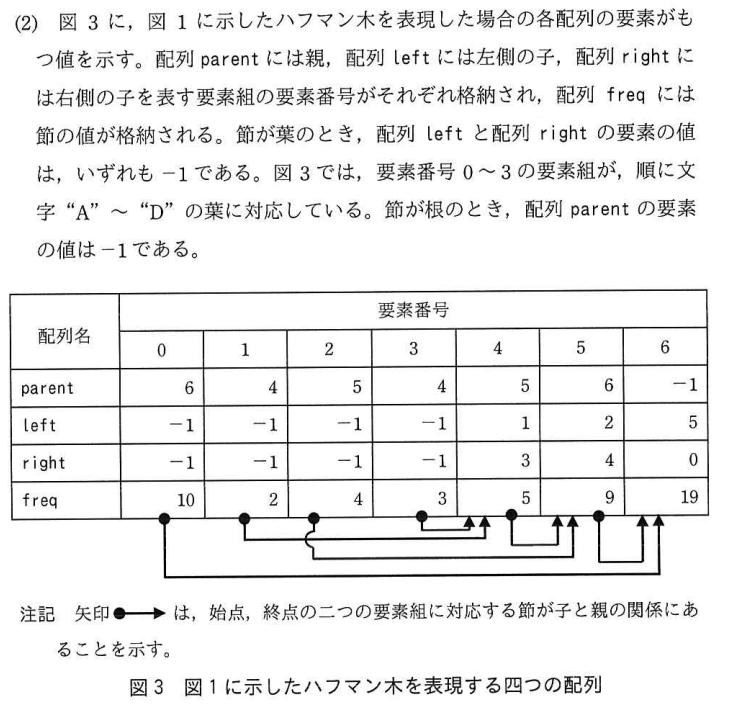
色々情報が出てきましたが一つずつかみ砕いていきましょう。
まず、今までの手順では文字と出現回数の配列を最初に作っていましたね。
それが図3のどこに当たるかを考えてみると…「freq」が出現頻度になります。(freqは頻度という意味のfrequencyからきています)
一旦見知った図に起こしてみて、他の3つの配列について考えていきます。
最初の「10」は「葉」なので左右はいません。よって初期値の-1が入っています。0~3番目までは同様にすべて-1ですね。
親は親の節を作成する次の手順で決まります。初期値で-1が入っていますがメモがぐちゃぐちゃになるので空欄とします。
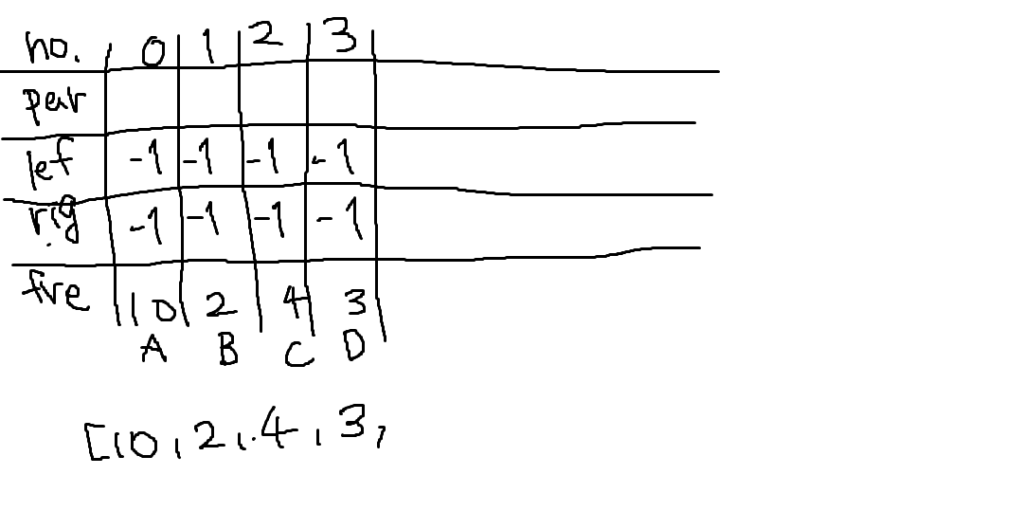
値の小さい節として1番目と3番目を選んで親の節を4番目に作ります。
1番と3番の親が4番になるので、1番と3番のparentには4が入ります。
そして4番のleftには左の節である1番が、rightには3番が入ります。
ここで注意点はfreqの配列には値が入りますが、他の配列には要素番号が入る点です。
似たような数字があると特に本番は混乱してしまうのでしっかり区別しましょう。
例えば要素番号のところは数字を「[ ]」で囲むなどで区別するといいと思います。
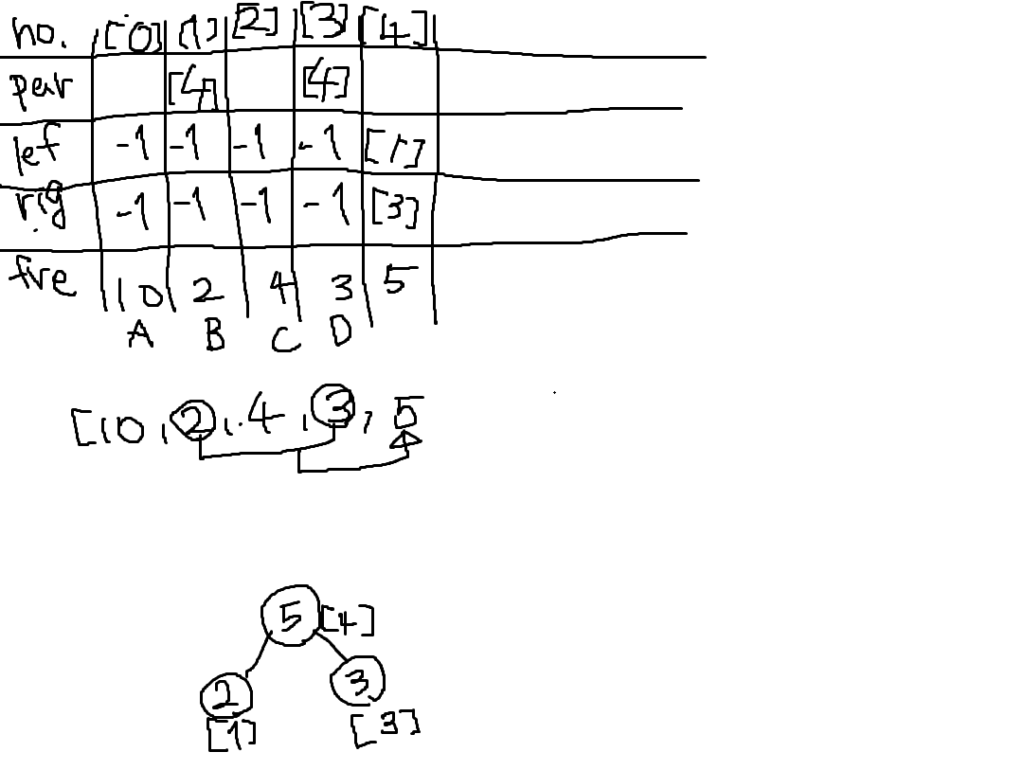
ハフマン木の最後(根ができるまで)考えても良いですが、完成形の図があるので原理が分かれば十分です。
プログラムの説明を読み進めます。


登場人物の説明です。
設問の選択肢にあった「size」が出てきました。これは要チェックです。

次の(4)では別のプログラムの説明です。
今まで日本語ベースで確認してきたものと比較するなら、親がいない節の値が1番小さい要素番号と2番目に小さい要素番号から親の節を作る作業に対して、ここでは親がいない節をすべて抜き出して昇順(小さい順)に並べています。
親の節の作成は、こっちのプログラムでは、日本語を見る限りはやらなそうです。
プログラムが複数ある場合は、どこからどこまでの処理をどの関数が担当しているかをしっかり区別しましょう。
ここで選択肢にあった「nsize」が出てきました。親がいない節の数になります。
行番号が書かれているので、プログラムのソースを読む際に日本語との対応付けが楽になってありがたいです。

次の説明に関するプログラムのソースはないみたいですね。
(4)で並び替えたものに従って要素組も並び替えるよと言っています。
ところで要素組。覚えていますか?私は結構文章の中特有の表現忘れがちです..。
4つの配列(parent, left, right, freq)で同じ要素番号を持つ組でした。
定義だったり曖昧だなと思うものは戻って確認しつつ進めましょう。
また、一度戻って確認したものはメモにさらっと書いておくとまた忘れたときに便利です。
入出力とソースコードを確認する
ようやくプログラムの引数の説明までたどり着きました。
とはいえ目新しい配列名や変数名はないのでさらっと確認する程度でOKです。

ソースが省略されているSortの引数仕様も書いてあります。こちらもさらっと確認でOKです。
ソースが省略されているものは、処理の内容は日本語で、入出力は呼び出し元のプログラムと関連付けして把握すると時間短縮になります。

いよいよソースコードの登場です!

上から順番に見ていきます。
まず、最初に渡されるのは初期化された4種の配列です。
freqに関しては葉の文字の出現回数は格納されている状態です。
これに対してSortNode関数を叩いています。
一旦詳しい処理フローはおいておいて、昇順に整列されたnode[]の配列が返ってきます。まだ親はいないのでnsizeは文字数と同じ4になります。
ここで空欄「c」の条件を満たすと後続の処理に続けます。
後続の処理のコメントを見ると、どうやら親の節を作成する処理を行い、14行目で親を一つ作成した後の配列に対してSortNodeをしているようです。
つまり、空欄「c」の条件には「親がいない節が2つ以上なら」が入りそうです。
この日本語見覚えありませんか?最初の方のハフマン木の作成手順にありました。

では選択肢の中からこれに当てはまりそうなものを検討してみましょう。

nsizeは整列対象、つまり親がいない節の数と同義でした。「ウ」が正解になります。
なんとトレースやプログラムを追うことなく、日本語やプログラムのコメントでほとんど解けてしまいました!
プログラミング未経験者でも安心ですね!
次のプログラムを見てみましょう。

こちらは親がいない節を抜き出して昇順に並べるプログラムでした。
事前に確認したプログラムの説明で、19行目~24行目が親が生成されていない節を抜き出すものだとわかっています。
18行目でnsizeを0で初期化し、19行目、20行目の条件に当てはまれば22行目で親がいない節のカウントを1追加しています。
19行目で変数 i は0~sizeで変化しているため要素番号だと推測できます。
空欄「d」の条件を満たせば、nodeの配列のnsize番目の値として要素組の要素番号である i が格納される流れです。
よって空欄「d」には「親がいない節である」という条件が入りそうです。
選択肢を見てみましょう。

まず「ア」~「ウ」は親がいない節の数であるnsizeを条件としているのでNGです。
「エ」と「オ」はparent[i]、つまり該当する要素番号の親の節の要素番号を表現しています。
親がいなければ初期値の-1となり、親がいればその要素番号になるので「親がいない」の条件判定に使えそうです。
不等号の向きに注意して空欄「d」の答えは「エ」になります。
こちらの問題は、配列の扱いに慣れていない人にとってはピンと来ない問題化もしれません。
アルゴリズム問題は配列を必ず使うので徐々に慣れていきましょう!
設問3を解く
次はビット列生成のプログラムに関する問題です。

またまたプログラムの穴埋めですね。
安定の日本語から理解をはじめましょう!
プログラムの説明を読む
最初の方の手順で確認した例を引っ張ると、文字Bに該当する要素番号(1番)を引数kに渡すと、ビット表現の「010」が表示されるイメージですね。
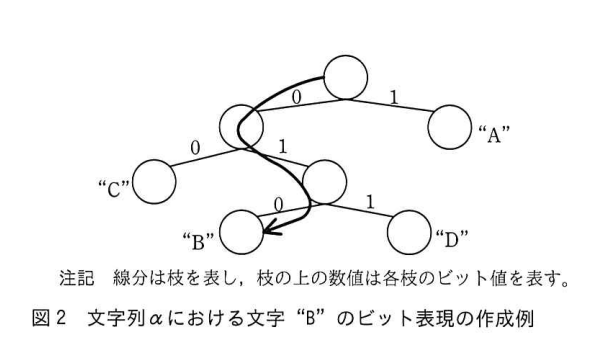
続きを読みます。

文字Bの節(葉)の要素番号を受け取って開始ですが、ビット表現自体は「根」から始まるので、文字Bの節から根まで登って、そこから降りてきてBの節まで戻ればゴールになります。
行番号2の条件は空欄「e」になっています。
説明では「根までたどっていく」「根にたどり着くと」という表現がされています。
根でなければEncodeを再帰的に呼び出すので、親がいれば呼び出すと言い換えられそうです。
アルゴリズム問題はこのようにちょっと日本語を言い換えればプログラムのコードに似た表現にすることができます。
選択肢に迷ったら、選択肢を日本語にしてみて説明文と合致しているかを確認するテクニックも使えます!
ハフマン木を図示するときは視覚的に左を0、右を1とできましたが、相手はプログラムなのでできません。
「現在の節が親の左側の子」をプログラムに分かるようにどう表現するかですね。
ちなみにここ、空欄「f」の箇所です。入れ子になっていたり複雑そうな部分を最後の問題に持ってくるとは受験生泣かせです。
では、プログラムと選択肢を見ていきましょう。
ソースコードと選択肢を見る
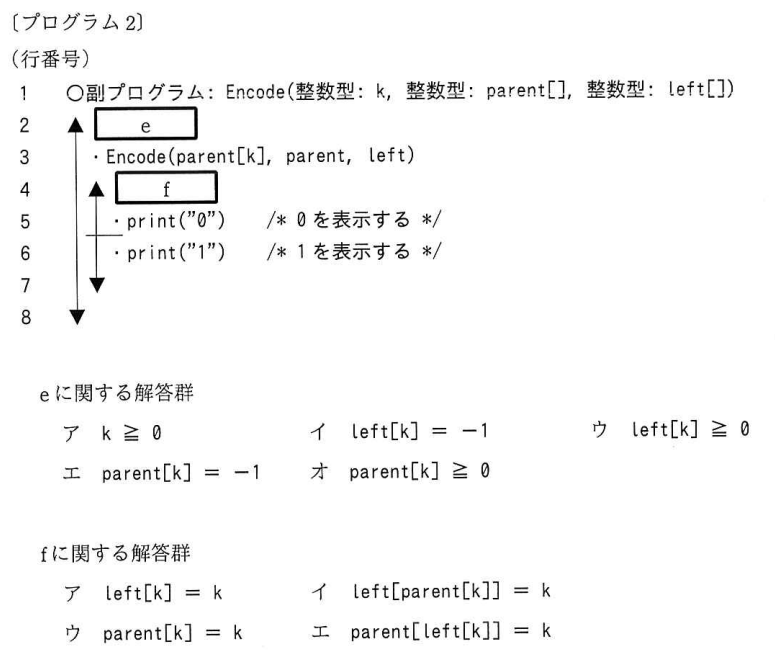
空欄「e」から解きます。
プログラムの説明から空欄「e」は「親がいれば」再帰的にEncodeを呼び出すとなると推測していました。
親に関する選択肢は「エ」と「オ」です。
「エ」は要素番号kの節の親がいない、つまり「根である」ことになるので呼び出し条件ではなく、呼び出しが終わる条件になってしまします。
一方「オ」は0以上と親の節を表現しているのでこちらが正解になります。
最後にラスボスの空欄「f」です。
「現在の節が親の左側の子」の表現に当てはまるものを探します。
一つ一つ分解すると、
- k:現在の節(要素番号)
- left[k]:現在の節(要素番号)の左の子の節(要素番号)
- parent[k]:現在の節(要素番号)の親の節(要素番号)
を表現しています。
よって、選択肢は下記のように書き換えることができます。
- ア:左の子=現在の節
- イ:現在の節の親の左の節=現在の節
- ウ:親の節=現在の節
- エ:現在の節の左の子の節の親=現在の節
このうち「現在の節が親の左側の子」に合致するのは「イ」になります。
文章で考えるとわかりにくいなと思う人は表を書いてみると理解が深まるかもしれません。
※ちなみに書きながら私も混乱しちゃうレベルです。ちょっと複雑だなと思ったら時間を惜しまずメモを取りましょう。
具体例として、上にも下にも節がある要素番号5番を例に考えてみます。(要素番号4番でもOKです。)

ちょっとメモがぐちゃぐちゃで赤線を使うズルをしてしまいましたが、ご自身で描かれたハフマン木や配列を辿り、選択肢が何を指しているか分かるレベルまで理解できれば復習・問題練習としては◎です!
おわりに
長丁場お疲れさまでした。
最後まで読んでくださりありがとうございます。
問題は解けましたか?
今回紹介した解き方がすべてのアルゴリズム問題に適応できるわけではありませんが、一つ一つ読み解いていけば合格へ近づきます。
少しでもアルゴリズム問題に対する苦手意識が減ってくれると嬉しいです。
最後に公式の講評を貼っておきます。ご自身の正答率と比較してみてください。




コメント